北極海氷分布予報2021年第三報補足:単回帰及び重回帰分析を用いた海氷予測の比較
第一報、第二報では、海氷上粒子の密度と海氷密接度の相関を見ることにより、予測計算を行いました。 第三報ではそれに海氷年齢という新たな変数を加えた重回帰分析により予測計算を行いました。 ここでは、その手法を説明するとともに、従来手法による予測結果との違いを解説します。
重回帰分析
第一報、第二報では4月末及び5月末の海氷上粒子の密度(直前の冬から春にかけての海氷厚変化を反映)と
海氷密接度の線形トレンドからの偏差の関係を単回帰分析により求め、予測に用いました。
第三報ではこれに海氷年齢を加えた重回帰分析を用いて予測計算を行いました。一般的に年齢の大きい海氷ほど厚いため、
粒子密度と比べてより長期の海氷厚変化を反映していると考えられます。海氷年齢の情報を予測に加えることにより、
何年もかけて成長した厚い氷の分布を考慮することができるようになります。
本解析では以下のような計算方法で重回帰式を求めました。
\begin{align*}
(SIC’)^{n}_{i,j} = a \cdot{} P^{n}_{i,j} + b \cdot{} (SIA)^{n}_{i,j} + c \tag{1}
\end{align*}
式$(1)$を求める重回帰式とします。
ここで、$SIC’$は回帰平面より求められる海氷密接度の線形トレンドからの偏差、
$P$は粒子の密度、$SIA$は海氷年齢、$n$は年、$i,j$は格子点の座標、
$a,b,c$は回帰平面を決定する定数で、この定数を最小二乗法を用いて求めます。
最小二乗法は回帰平面と実測値との偏差の二乗和が最小になるように各定数を決定する方法であるため、
式$(2)$を各定数で偏微分したものが$0$となる$a,b,c$を求めることになります。
\begin{align*}
\sum_{\begin{matrix}
7 \le n \le 11 \\
16 \le n \le 20\
\end{matrix}}
(SIC’)^{n}_{i,j} = ((SIC)^n-(SIC’)^n)^2 =
\sum_{\begin{matrix}
7 \le n \le 11 \\
16 \le n \le 20\
\end{matrix}}
(a \cdot{} P^{n} + b \cdot{} (SIA)^{n} + c – (SIC’)^n)^2 \tag{2}
\end{align*}
ここで、$SIC$は海氷密接度の線形トレンドからの偏差です。
また位置に関しては固定して考えているため、$i,j$の添え字を省略しています。
式$(2)$を偏微分し$0$となる条件を付加させた結果をまとめると式$(3)$のような三元一次連立方程式が導かれ、
これを解くことによって回帰平面を決定する定数$a,b,c$を得ることができます。
\begin{align*}
\left\{
\begin{array}{l}
aS_{xx} + bS_{xy} + cS_{x} = S_{xz} \\
aS_{yy} + bS_{xy} + cS_{y} = S_{yz} \tag{3}\\
aS_{x} + bS_{y} + cn = S_{z} \\
\end{array}
\right.
\end{align*}
\begin{align*}
S_{x}=
\sum_{\begin{matrix}
7 \le n \le 11 \\
16 \le n \le 20\
\end{matrix}}
(P^{n}),
\qquad
S_{y}=
\sum_{\begin{matrix}
7 \le n \le 11 \\
16 \le n \le 20\
\end{matrix}}
((SIA)^{n}),
\qquad
S_{z}=
\sum_{\begin{matrix}
7 \le n \le 11 \\
16 \le n \le 20\
\end{matrix}}
((SIC’)^{n}),
\end{align*}
\begin{align*}
S_{xx}=
\sum_{\begin{matrix}
7 \le n \le 11 \\
16 \le n \le 20\
\end{matrix}}
(P^{n})^{2},
\qquad
S_{yy}=
\sum_{\begin{matrix}
7 \le n \le 11 \\
16 \le n \le 20\
\end{matrix}}
((SIA)^{n})^{2},
\end{align*}
\begin{align*}
S_{xy}=
\sum_{\begin{matrix}
7 \le n \le 11 \\
16 \le n \le 20\
\end{matrix}}
(P^{n} \cdot (SIA)^{n}),
\qquad
S_{xz}=
\sum_{\begin{matrix}
7 \le n \le 11 \\
16 \le n \le 20\
\end{matrix}}
(P^{n} \cdot (SIC’)^{n}),
\qquad
S_{yz}=
\sum_{\begin{matrix}
7 \le n \le 11 \\
16 \le n \le 20\
\end{matrix}}
((SIA)^{n} \cdot (SIC’)^{n})
\end{align*}
本解析では連立方程式の解法はクラメルの公式を用いました。
以上より求めた回帰平面で今年の線形トレンドからの偏差を求め、
今年の線形トレンドに足し合わせることにより、後述の図1右のような解析結果を得ています。
海氷分布

図1は2021年6月30日の海氷の状況を考慮した7月1日から9月20日の海氷予測で、左が第一報、第二報で用いた方法で求めた海氷予測、 右が第三報で用いた方法の海氷予測です。両者を見比べるとカラ海周辺では大きな差がないものの、 ラプテフ海周辺では単回帰分析を用いた方法の方が重回帰分析を用いた方法に比べて海氷の減りが大きいことがわかります。 また、重回帰分析による結果ではボーフォート海に海氷が残りやすくなっています。これらの差が生まれるひとつの原因として、 単回帰分析と重回帰分析で用いたデータの年数が違うことが考えられます。 重回帰分析に用いる海氷年齢は過去4年に亘って遡って計算するためデータの利用できる年数が少なくなります。 具体的には、単回帰分析では2012年を除いた2003年から2020年までの17年分のデータを用いて計算しているのに対し、 重回帰分析では2007年から2011年、2016年から2020年までの10年分のデータを用いて計算しています。
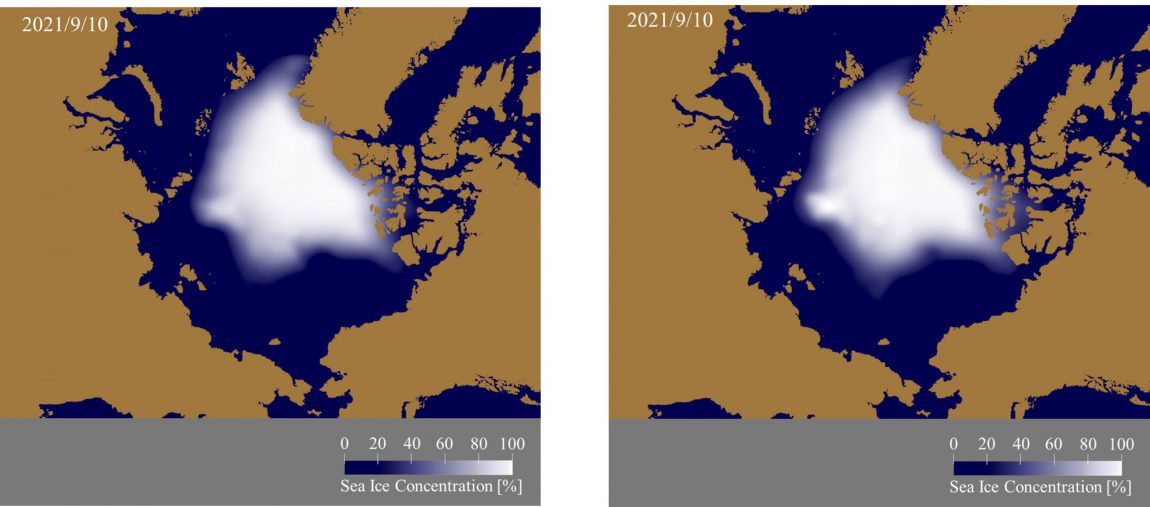
右:2007年から2011年までと2016年から2020年までの10年分を考慮した結果。
単回帰分析に用いるデータ数を重回帰分析と同じにした場合(図2)、ラプテフ海周辺の海氷減少の速さは重回帰分析の結果と近くなります。 一方、ボーフォート海周辺では単回帰分析に用いるデータの年数を変えても予測に大きな変化が見られません。 このことから、重回帰分析による予測結果に見られるボーフォート海の海氷後退の遅れは、用いるデータ数が少ないことによるものではなく、 年月を経た多年氷の影響を反映したものと考えられます。


